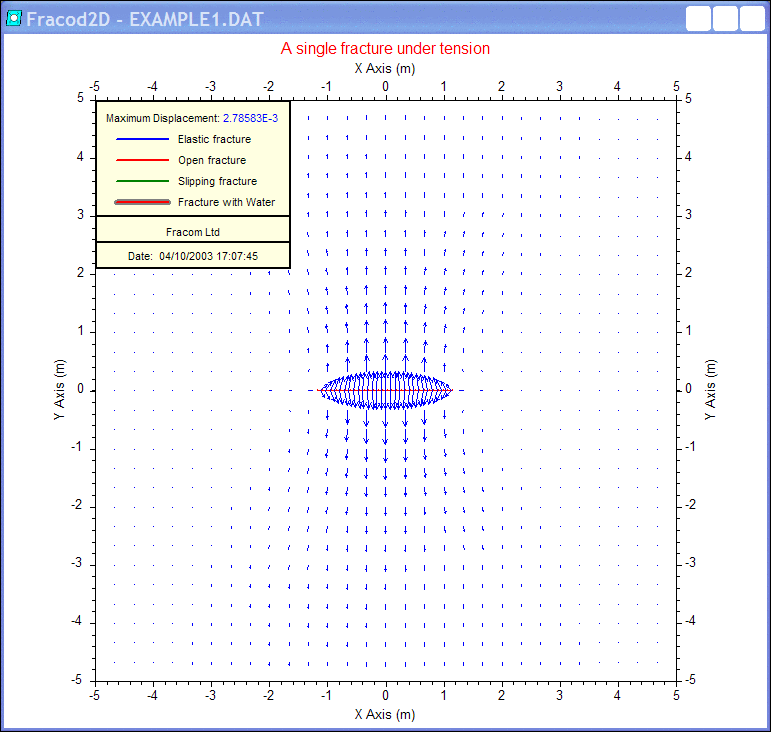
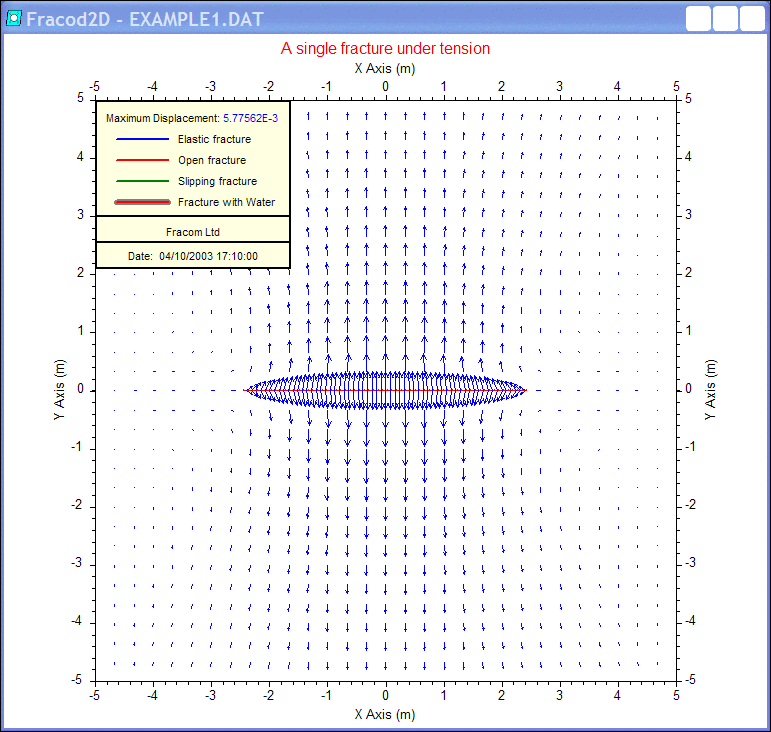
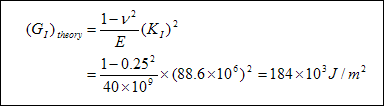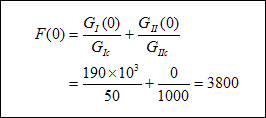A 2m fracture in an infinite rock mass is under uniaxial tensile stress of 50MPa in the direction perpendicular to the fracture plane. The elastic properties of the rock mass are:
E = 40GPa
v = 0.25.
The strain energy release rate in mode I for this problem is calculated by using the FRACOD2D code with 30 elements along the fracture.
(GI)FRACOD = 190×103 J/m2
The theoretical solution of this problem gives the stress intensity factor (KI) as
where a = half length of the fracture.
The theoretical strain energy release rate is then calculated as:
The difference between the numerical result and the theoretical result is approximately 3%.
In this example, the critical strain energy release rates of fracture propagation are:
GIc =50 J/m2
GIIc =1000 J/m2 .
As the fracture propagation is pure mode I along the fracture's original plane, only the critical strain energy release rate in mode I (GIc) is useful. The F-value obtained from the FRACOD2D modelling is:
The F-value is by far greater than the critical value 1.0. Hence fracture propagation is detected.